Sifat-sifat Elementer Ring – STRUKTUR ALJABAR

Diberikan ring $(R,+,\cdot)$ . Dari ddefinisi ring, diperoleh bahwa $(R,+)$ merupakan grup. Dengan demikian, pada $R$ terdapat elemen nol \index{elemen nol} $0_R$ sedemikian sehingga untuk setiap $r$ di $R$ memenuhi:

$0_R+r=r+0_R=r,$

dan untuk setiap elemen $r\in R$ terdapat $-r \in R$ sedemikian hingga

$r+(-r)=(-r)+r=0_R.$

Selanjutnya, untuk mempersingkat penulisan, perkalian $r_1\cdot r_2$ dapat ditulis $r_1 r_2$ dan penjumlahan $r_{1}+(-r_{2})$ dapat ditulis $r_{1}-r_{2}$ . Berikut sifat-sifat dasar dari ring $R$ dalam kaitannya dengan operasi perkaliannya.

Teorema 1. Jika ( $R,+,\cdot$ ) merupakan ring maka berlaku sifat-sifat sebagai berikut:

untuk setiap $r \in R$ , $r 0_R=0_R r = 0_R$ ;
untuk setiap $r_1, r_2 \in R$ , $(-r_1) r_2= - (r_1 r_2)= r_1 (- r_2)$ ;
untuk setiap $r_1, r_2 \in R$ , $(-r_1) (-r_2)= r_1 r_2$ ;
untuk setiap $r_1, r_2, r_3\in R$ , $r_1(r_2 - r_3)=r_1r_2 - r_1r_3$ dan $(r_2 - r_3)r_1=r_2r_1-r_3r_1$ .

Bukti.

Diambil sebarang 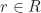$r\in R$ . Berdasarkan sifat distributif dan sifat elemen nol, diperoleh $r0_R+r0_R=r(0_R+0_R)=r0_R$ . Perhatikan bahwa
$\begin{eqnarray*} &(r0_R+r0_R)+(-(r0_R))&=r0_R+(-(r0_R))\\ &r0_R+(r0_R+(-(r0_R)))&=0_R\\ &\hspace{2.5cm}r0_R+0_R&=0_R, \end{eqnarray*}$

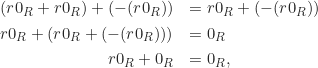
sehingga diperoleh $r0_R=0_R$ .
Selanjutnya, diambil sebarang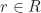 $r\in R$ . Berdasarkan sifat distributif dan elemen nol, diperoleh $0_Rr+0_Rr=(0_R+0_R)r=0_Rr$ . Perhatikan bahwa

$\begin{eqnarray*} &(0_Rr+0_Rr)+(-(0_Rr))&=0_Rr+(-(0_Rr))\\ &0_Rr+(0_Rr+(-(0_Rr)))&=0_R\\ &\hspace{2.5cm}0_Rr+0_R&=0_R, \end{eqnarray*}$

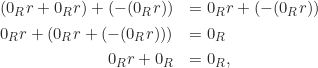
sehingga diperoleh $0_Rr=0_R$ .
Diambil sebarang 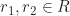$r_1, r_2 \in R$ . Berdasarkan sifat distributif, diperoleh
$\begin{eqnarray*} r_1r_2+(-r_1)r_2&=&(r_1+(-r_1))r_2=0_Rr_2\\ &=&0_R\\ &=&0_Rr_2=(-r_1+r_1)r_2=(-r_1)r_2+r_1r_2 \end{eqnarray*}$

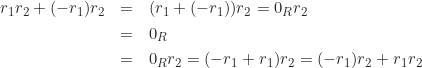
dan

$\begin{eqnarray*} r_1r_2+r_1(-r_2)&=&r_1(r_2+(-r_2))=r_10_R\\ &=&0_R\\ &=&r_10_R=r_1(-r_2+r_2)=r_1(-r_2)+r_1r_2. \end{eqnarray*}$

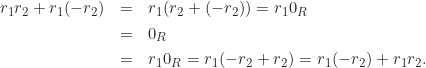
Karena elemen invers dari 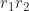$r_1r_2$ adalah 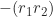$-(r_1r_2)$ dan elemen invers bersifat tunggal, diperoleh

$(-r_1)r_2=-(r_1r_2)=r_1(-r_2).$
Diambil sebarang 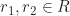$r_1, r_2 \in R$ . Dengan menggunakan sifat (ii), diperoleh
$(-r_1)(-r_2)=-(r_1(-r_2))=-(-(r_1r_2))=r_1r_2.$
Diambil sebarang 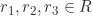$r_1, r_2,r_{3} \in R$ . Karena 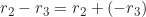$r_2-r_3=r_2+(-r_3)$ , diperoleh
$\begin{align*} r_1(r_2 - r_3) &= r_1 (r_2+(-r_3))=r_1r_2+r_1(-r_3)\\ &= r_1r_2+(-(r_1r_3))=r_1r_2 - r_1r_3. \end{align*}$

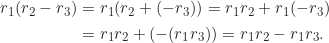
Secara analog, dapat dibuktikan $(r_2 - r_3)r_1=r_2r_1-r_3r_1$ .

$\blacksquare$

Pada ring ( $\mathbb{Z},+,\cdot$ ), terdapat elemen $1\in\mathbb{Z}$ sedemikian sehingga bersifat $1r=r=r1$ untuk setiap $r\in\mathbb{Z}$ . Berbeda dengan ring ( $2\mathbb{Z},+,\cdot$ ), tidak ada elemen $e\in 2\Z$ sedemikian sehingga untuk setiap $r\in R$ berlaku $er=r=re$ . Selanjutnya, untuk sebarang ring $(R,+,\cdot)$ , suatu elemen $e\in R$ disebut\index{elemen satuan} elemen satuan jika untuk setiap $r\in R$ berlaku sifat $er=r=re$ .
Jika diperhatikan kembali ring ( $\mathbb{Z},+,\cdot$ ) dan ( $2\mathbb{Z},+,\cdot$ ) maka tampak bahwa ring $\Z$ memiliki elemen satuan, sedangkan ring $2\Z$ tidak memiliki elemen satuan. Dengan demikian, dapat disimpulkan bahwa secara umum struktur ring belum tentu memuat elemen satuan terhadap operasi perkaliannya. Elemen satuan dalam suatu ring $R$ (jika ada) biasanya dinotasikan dengan $1_R$ .

Teorema 2. Diketahui $(R,+,\cdot)$ ring dengan elemen satuan $1_{R}$ dan memiliki lebih dari satu anggota. Maka berlaku $1_{R}\neq 0_{R}$ .

Bukti. Andaikan $1_{R}=0_{R}$ . Karena $R$ memiliki lebih dari satu anggota, maka ada $r\in R$ dengan $r\neq 1_{R}$ dan $r\neq 0_{R}$ . Diperhatikan bahwa $r=r1_{R}=r0_{R}=0_{R}$ . Kontradiksi dengan $r\neq 0_{R}$ . Jadi haruslah $1_{R}\neq 0_{R}$ .

$\blacksquare$