 Kita perhatikan kembali bahwa pada artikel sebelumnya telah dibahas definisi grup yang merupakan abstraksi dari fenomena-fenomena yang kita temui dalam bermatematika di kehidupan sehari-hari, salah satunya adalah fenomena dalam himpunan
Kita perhatikan kembali bahwa pada artikel sebelumnya telah dibahas definisi grup yang merupakan abstraksi dari fenomena-fenomena yang kita temui dalam bermatematika di kehidupan sehari-hari, salah satunya adalah fenomena dalam himpunan ![]() yang dilengkapi operasi penjumlahan
yang dilengkapi operasi penjumlahan ![]() . Misal diberikan suatu grup
. Misal diberikan suatu grup ![]() . Bagi para pembaca yang baru pertama kali belajar struktur aljabar, untuk mempelajari sifat-sifat elementer dari grup
. Bagi para pembaca yang baru pertama kali belajar struktur aljabar, untuk mempelajari sifat-sifat elementer dari grup ![]() secara langsung nampaknya sulit sebab himpunan
secara langsung nampaknya sulit sebab himpunan ![]() tersebut sifatnya abstrak, tidak diketahui secara pasti bentuk elemen-elemennya, apakah berupa bilangan, matriks, fungsi, atau yang lainnya. Mengingat munculnya definisi grup tersebut termotivasi dari
tersebut sifatnya abstrak, tidak diketahui secara pasti bentuk elemen-elemennya, apakah berupa bilangan, matriks, fungsi, atau yang lainnya. Mengingat munculnya definisi grup tersebut termotivasi dari ![]() yang dilengkapi operasi penjumlahan
yang dilengkapi operasi penjumlahan ![]() , untuk mempelajari sifat-sifat elementer dari grup akan lebih mudah jika kita juga berangkat dari grup bilangan bulat
, untuk mempelajari sifat-sifat elementer dari grup akan lebih mudah jika kita juga berangkat dari grup bilangan bulat ![]() .
.
Kita perhatikan bahwa dalam grup bilangan bulat ![]() hanya terdapat satu elemen netral, yaitu
hanya terdapat satu elemen netral, yaitu ![]() . Hal ini dapat juga kita katakan bahwa elemen netral dalam grup
. Hal ini dapat juga kita katakan bahwa elemen netral dalam grup ![]() tunggal. Selain itu, kita perhatikan juga bahwa untuk setiap elemen di dalam grup
tunggal. Selain itu, kita perhatikan juga bahwa untuk setiap elemen di dalam grup ![]() mempunyai tepat satu elemen invers, sebagai contoh: invers
mempunyai tepat satu elemen invers, sebagai contoh: invers ![]() adalah
adalah ![]() , tidak ada elemen lain selain
, tidak ada elemen lain selain ![]() di
di ![]() yang merupakan invers dari 1. Pernyataan ini secara ringkas dapat kita katakan bahwa invers setiap elemen di dalam grup
yang merupakan invers dari 1. Pernyataan ini secara ringkas dapat kita katakan bahwa invers setiap elemen di dalam grup ![]() tunggal. Kedua sifat tersebut selanjutnya perlu kita lihat keberlakuannya pada sebarang grup
tunggal. Kedua sifat tersebut selanjutnya perlu kita lihat keberlakuannya pada sebarang grup ![]() . Perhatikan lemma berikut.
. Perhatikan lemma berikut.
Lemma. Jika ![]() merupakan grup, maka:
merupakan grup, maka:
- elemen netral di dalam
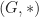 tunggal;
tunggal; - invers setiap elemen dalam
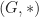 tunggal.
tunggal.
Bukti.
- Misal
 dan
dan 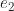 masing-masing adalah elemen netral di dalam grup
masing-masing adalah elemen netral di dalam grup  . Karena
. Karena  merupakan elemen netral dan
merupakan elemen netral dan 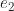 adalah suatu elemen di
adalah suatu elemen di  , diperoleh
, diperoleh  . Karena
. Karena 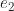 merupakan elemen netral dan
merupakan elemen netral dan  adalah suatu elemen di
adalah suatu elemen di  , diperoleh
, diperoleh  . Dengan demikian, diperoleh kesimpulan
. Dengan demikian, diperoleh kesimpulan
![Rendered by QuickLaTeX.com \[e_1=e_1e_2=e_2.\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-7f7c3502db1f66035863df44dfb88b3b_l3.png)
Jadi, terbukti bahwa elemen netral di dalam grup
 tunggal.
tunggal. - Diambil sebarang
 di dalam
di dalam  . Misal
. Misal  dan
dan 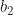 masing-masing adalah elemen di dalam
masing-masing adalah elemen di dalam  yang merupakan invers dari elemen
yang merupakan invers dari elemen  . Hal ini berarti
. Hal ini berarti  dan
dan  . Perhatikan bahwa
. Perhatikan bahwa
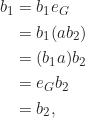
sehingga terbukti ketunggalan invers setiap elemen di dalam
 .
. 
Selanjutnya, apabila dipunyai ![]() , mudah kita pahami bahwa
, mudah kita pahami bahwa ![]() dan
dan ![]() . Seperti apakah invers dari masing-masing elemen
. Seperti apakah invers dari masing-masing elemen ![]() dan
dan ![]() tersebut? Perhatikan lemma berikut.
tersebut? Perhatikan lemma berikut.
Lemma. Diberikan grup ![]() .
.
- Jika
 maka
maka  .
. - Jika
 maka
maka  .
.
Bukti.
- Diketahui
 . Akan ditunjukkan bahwa
. Akan ditunjukkan bahwa  merupakan invers dari
merupakan invers dari  .
.
Perhatikan bahwa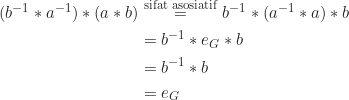
dan
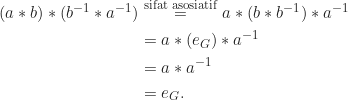
Jadi, terbukti bahwa
 merupakan invers dari
merupakan invers dari  , atau dengan kata lain
, atau dengan kata lain  .
. - Diketahui
 . Telah kita ketahui bahwa invers dari elemen
. Telah kita ketahui bahwa invers dari elemen  dinotasikan
dinotasikan  . Hal ini berarti
. Hal ini berarti  . Dari persamaan tersebut, mudah dipahami bahwa
. Dari persamaan tersebut, mudah dipahami bahwa  merupakan invers dari elemen
merupakan invers dari elemen  . Karena ketunggalan invers dari elemen di dalam grup dan
. Karena ketunggalan invers dari elemen di dalam grup dan  merupakan notasi untuk invers elemen
merupakan notasi untuk invers elemen  , diperoleh kesimpulan bahwa
, diperoleh kesimpulan bahwa  .
. 
Sifat lain yang perlu kita lihat pada grup ![]() adalah sifat kanselasi, yaitu untuk setiap
adalah sifat kanselasi, yaitu untuk setiap ![]() , jika
, jika ![]() maka berakibat
maka berakibat ![]() . Ternyata sifat ini juga berlaku untuk sebarang grup
. Ternyata sifat ini juga berlaku untuk sebarang grup ![]() .
.
Teorema. Diberikan grup ![]() dan sebarang
dan sebarang ![]() .
.
- Jika
 maka
maka  . (kanselasi kanan)
. (kanselasi kanan) - Jika
 maka
maka  . (kanselasi kiri)
. (kanselasi kiri)
