 Dalam kehidupan sehari-hari, kita telah mengenal dan menggunakan berbagai operasi bilangan. Untuk lebih mudahnya, kita dapat mengambil satu contoh, yaitu operasi penjumlahan bilangan bulat, yang sering kita gunakan dalam menghitung banyaknya uang (rupiah) yang kita punyai. Apabila kita mempunyai satu lembar uang
Dalam kehidupan sehari-hari, kita telah mengenal dan menggunakan berbagai operasi bilangan. Untuk lebih mudahnya, kita dapat mengambil satu contoh, yaitu operasi penjumlahan bilangan bulat, yang sering kita gunakan dalam menghitung banyaknya uang (rupiah) yang kita punyai. Apabila kita mempunyai satu lembar uang ![]() dan satu lembar uang
dan satu lembar uang ![]() , maka total uang yang kita punyai adalah
, maka total uang yang kita punyai adalah ![]() . Dalam perhitungan jumlahan tersebut, yang kita lakukan sebenarnya adalah mengoperasikan dua bilangan di dalam himpunan
. Dalam perhitungan jumlahan tersebut, yang kita lakukan sebenarnya adalah mengoperasikan dua bilangan di dalam himpunan ![]() dan selanjutnya kita mendapatkan hasil berupa bilangan yang termuat di dalam himpunan
dan selanjutnya kita mendapatkan hasil berupa bilangan yang termuat di dalam himpunan ![]() . Pehitungan ini dikenal sebagai operasi penjumlahan bilangan bulat.
. Pehitungan ini dikenal sebagai operasi penjumlahan bilangan bulat.
Perhatikan bahwa bentuk pengoperasian jumlahan dua bilangan bulat seperti yang dicontohkan di atas, secara matematis dapat kita lihat sebagai suatu fungsi dengan domain ![]() dan kodomain
dan kodomain ![]() . Fungsi tersebut dinotasikan dengan simbol
. Fungsi tersebut dinotasikan dengan simbol ![]() . Dengan demikian, secara ringkas, operasi bilangan bulat adalah suatu fungsi
. Dengan demikian, secara ringkas, operasi bilangan bulat adalah suatu fungsi
![]()
Mungkin para pembaca kurang familiar dengan notasi ![]() di atas, sebab notasi fungsi yang sering kita jumpai menggunakan huruf
di atas, sebab notasi fungsi yang sering kita jumpai menggunakan huruf ![]() ,
, ![]() , dan lain sebagainya. Notasi
, dan lain sebagainya. Notasi ![]() tersebut memberi makna suatu elemen di
tersebut memberi makna suatu elemen di ![]() yang merupakan hasil peta dari elemen
yang merupakan hasil peta dari elemen ![]() oleh fungsi
oleh fungsi ![]() . Mengingat dalam pembicaraan ini yang dimaksud fungsi
. Mengingat dalam pembicaraan ini yang dimaksud fungsi ![]() adalah operasi penjumlahan bilangan bulat, notasi
adalah operasi penjumlahan bilangan bulat, notasi ![]() juga dapat dinotasikan dengan notasi
juga dapat dinotasikan dengan notasi ![]() . Jadi, dalam konteks pembicaraan ini,
. Jadi, dalam konteks pembicaraan ini, ![]() dan
dan ![]() merupakan barang yang sama. Sebagai contoh,
merupakan barang yang sama. Sebagai contoh,
![]() .
.
Berdasarkan fenomena tersebut, yakni operasi penjumlahan bilangan bulat ![]() yang dapat dipandang sebagai fungsi
yang dapat dipandang sebagai fungsi ![]() , kita lakukan suatu proses abstraksi sebagai berikut.
, kita lakukan suatu proses abstraksi sebagai berikut.
- Himpunan
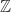 diabstraksikan menjadi sebarang himpunan tak kosong
diabstraksikan menjadi sebarang himpunan tak kosong 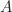 .
. - Fungsi
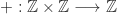 diabstraksikan menjadi sebarang fungsi
diabstraksikan menjadi sebarang fungsi

Fungsi ![]() ini selanjutnya disebut operasi biner pada himpunan tak kosong
ini selanjutnya disebut operasi biner pada himpunan tak kosong ![]() . Kata “biner” berasal dari kata binary atau
. Kata “biner” berasal dari kata binary atau ![]() –ary, yang dalam konteks ini mempunyai makna pengoperasian dilakukan untuk setiap dua pasangan berurutan
–ary, yang dalam konteks ini mempunyai makna pengoperasian dilakukan untuk setiap dua pasangan berurutan ![]() di dalam
di dalam ![]() .
.
Contoh:
- Dari penjelasan di atas, jelas bahwa operasi penjumlahan bilangan bulat
 merupakan operasi binear pada
merupakan operasi binear pada 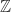 .
. - Operasi penjumlahan bilangan rasional
 merupakan operasi biner pada
merupakan operasi biner pada  .
. - Operasi penjumlahan bilangan real
 merupakan operasi biner pada
merupakan operasi biner pada 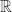 .
. - Operasi penjumlahan bilangan bulat
 bukan operasi biner pada himpunan semua bilangan ganjil
bukan operasi biner pada himpunan semua bilangan ganjil 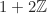 , sebab
, sebab 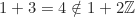 , yang berarti
, yang berarti  bukanlah fungsi dari
bukanlah fungsi dari  ke
ke 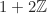 .
.
Kita perhatikan kembali himpunan tak kosong ![]() . Dari uraian penjelasan di atas, kita dapat membuat kesimpulan bahwa suatu pengaitan/relasi
. Dari uraian penjelasan di atas, kita dapat membuat kesimpulan bahwa suatu pengaitan/relasi ![]() dari
dari ![]() ke
ke ![]() disebut operasi biner jika
disebut operasi biner jika ![]() merupakan fungsi dari
merupakan fungsi dari ![]() ke
ke ![]() . Dengan demikian, untuk mengecek apakah suatu pengaitan
. Dengan demikian, untuk mengecek apakah suatu pengaitan ![]() dari
dari ![]() ke
ke ![]() merupakan operasi biner atau bukan, cukup dicek kebenaran dua pernyataan berikut:
merupakan operasi biner atau bukan, cukup dicek kebenaran dua pernyataan berikut:
- (Ketertutupan Hasil Operasi) Untuk setiap
 ,
,  berada di dalam
berada di dalam 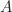 .
. - (Ketunggalan Hasil Operasi/Well-Defined)
Untuk setiap ![]() , apabila
, apabila ![]() maka berakibat
maka berakibat ![]()
Pernyataan no.2 di atas memberikan pengertian bahwa hasil operasi ![]() tidak bergantung pada notasi/simbol elemen yang kita ambil untuk menyatakan elemen di himpunan
tidak bergantung pada notasi/simbol elemen yang kita ambil untuk menyatakan elemen di himpunan ![]() . Pernyataan tersebut dapat juga dinyatakan sebagai berikut:
. Pernyataan tersebut dapat juga dinyatakan sebagai berikut:
Untuk setiap
, apabila
maka
Contoh:
- Diberikan himpunan

 , dan didefinisikan operasi
, dan didefinisikan operasi  dengan definisi
dengan definisi  untuk setiap
untuk setiap  . Akan dicek apakah
. Akan dicek apakah  merupakan operasi biner pada
merupakan operasi biner pada  .
.
Pertama, dicek apakah untuk setiap ![]() berlaku
berlaku ![]() . Diambil sebarang
. Diambil sebarang ![]() , hal ini berarti
, hal ini berarti ![]() dan
dan ![]() . Jelas bahwa
. Jelas bahwa ![]() , sehingga tinggal ditunjukkan bahwa
, sehingga tinggal ditunjukkan bahwa ![]() . Andaikan
. Andaikan ![]() , berarti
, berarti ![]() . Dengan menjumlahkan kedua ruas persamaan terakhir tersebut dengan 1, diperoleh
. Dengan menjumlahkan kedua ruas persamaan terakhir tersebut dengan 1, diperoleh ![]() . Hal tersebut berakibat
. Hal tersebut berakibat ![]() atau
atau ![]() , yang kontradiksi dengan fakta bahwa
, yang kontradiksi dengan fakta bahwa ![]() . Dengan demikian pengandaian salah, yang benar adalah
. Dengan demikian pengandaian salah, yang benar adalah ![]() . Jadi, terbukti bahwa
. Jadi, terbukti bahwa ![]() .
.
Kedua, dicek apakah operasi ![]() well-defined. Diambil sebarang
well-defined. Diambil sebarang ![]() dengan
dengan ![]() dan
dan ![]() . Perhatikan bahwa
. Perhatikan bahwa
![]()
Dengan demikian, operasi ![]() well-defined.
well-defined.
Kesimpulan: ![]() merupakan operasi biner pada
merupakan operasi biner pada ![]() .
.
