 Dalam artikel ini kita akan membahas tentang definisi dari salah satu jenis struktur aljabar, yakni grup. Dalam konteks ini, “grup” hanyalah suatu nama dari sistem yang akan kita pelajari. Seperti yang telah dipaparkan dalam judul artikel ini, grup merupakan suatu bentuk abstraksi dari suatu sistem tertentu.
Dalam artikel ini kita akan membahas tentang definisi dari salah satu jenis struktur aljabar, yakni grup. Dalam konteks ini, “grup” hanyalah suatu nama dari sistem yang akan kita pelajari. Seperti yang telah dipaparkan dalam judul artikel ini, grup merupakan suatu bentuk abstraksi dari suatu sistem tertentu.
Sekarang kita perhatikan himpunan semua bilangan bulat
![]()
dan operasi penjumlahan bi\-langan bulat ![]() . Mudah kita pahami bahwa
. Mudah kita pahami bahwa ![]() terhadap operasi
terhadap operasi ![]() memenuhi kaidah-kaidah:
memenuhi kaidah-kaidah:
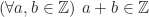
(sifat ketertutupan operasi )
)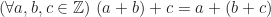
(sifat asosiatif)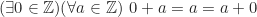
(adanya suatu elemen yang istimewa di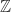 , yaitu
, yaitu  )
)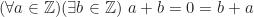
(setiap elemen di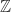 mempunyai pasangan di
mempunyai pasangan di 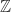 , yang apabila pasangan tersebut dioperasikan menghasilkan
, yang apabila pasangan tersebut dioperasikan menghasilkan  )
)
Berdasarkan hal tersebut, kita dapat mengatakan bahwa himpunan ![]() terhadap operasi penjumlahan
terhadap operasi penjumlahan ![]() membentuk suatu sistem.
membentuk suatu sistem.
PROSES ABSTRAKSI DAN PENDEFINISIAN STRUKTUR GRUP
Apakah hanya himpunan ![]() terhadap operasi penjumlahan
terhadap operasi penjumlahan ![]() saja yang memenuhi sifat/kaidah (i) sampai (iv) seperti di atas? Tentu saja tidak demikian, sebagai contoh:
saja yang memenuhi sifat/kaidah (i) sampai (iv) seperti di atas? Tentu saja tidak demikian, sebagai contoh: ![]() terhadap operasi
terhadap operasi ![]() ,
, ![]() terhadap operasi
terhadap operasi ![]() , himpunan semua matriks
, himpunan semua matriks ![]() , yaitu
, yaitu ![]() , terhadap operasi penjumlahan matriks
, terhadap operasi penjumlahan matriks ![]() , dan lain sebagainya. Dalam bermatematika, biasanya kita ingin melihat suatu jenis sistem secara luas. Oleh karena itu, untuk melihat dan mempelajari sistem seperti di atas (
, dan lain sebagainya. Dalam bermatematika, biasanya kita ingin melihat suatu jenis sistem secara luas. Oleh karena itu, untuk melihat dan mempelajari sistem seperti di atas (![]() terhadap operasi penjumlahan
terhadap operasi penjumlahan ![]() ) secara luas, kita lakukan proses abstraksi dari sistem tersebut.
) secara luas, kita lakukan proses abstraksi dari sistem tersebut.
![]()
![]()
Definisi. Diberikan himpunan tak kosong ![]() , dan pada
, dan pada ![]() didefinisikan suatu operasi biner
didefinisikan suatu operasi biner ![]() . Himpunan
. Himpunan ![]() disebut grup terhadap operasi
disebut grup terhadap operasi ![]() jika memenuhi sifat:
jika memenuhi sifat:
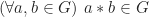
(sifat tertutup)1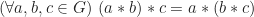
(sifat asosiatif)
(eksistensi elemen netral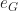 )
)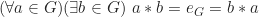 .
.
(eksistensi elemen invers untuk setiap elemen di )
)
Grup ![]() terhadap operasi biner
terhadap operasi biner ![]() secara ringkas dinotasikan dengan
secara ringkas dinotasikan dengan ![]() . Jika operasi biner
. Jika operasi biner ![]() pada grup
pada grup ![]() bersifat komutatif, yakni memenuhi
bersifat komutatif, yakni memenuhi ![]() , maka
, maka ![]() disebut grup abelian atau grup komutatif. Untuk efisiensi penulisan, penulisan
disebut grup abelian atau grup komutatif. Untuk efisiensi penulisan, penulisan ![]() secara singkat dapat ditulis
secara singkat dapat ditulis ![]() apabila notasi singkat ini tidak menimbulkan kerancuan.
apabila notasi singkat ini tidak menimbulkan kerancuan.
Contoh:
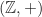 ,
,  ,
,  , dan
, dan 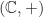 masing-masing merupakan grup (komutatif).
masing-masing merupakan grup (komutatif). ,
, 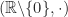 , dan
, dan 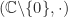 masing-masing merupakan grup (komutatif).
masing-masing merupakan grup (komutatif).
 merupakan grup terhadap operasi
merupakan grup terhadap operasi  dengan definisi
dengan definisi  untuk setiap
untuk setiap  .
.
Petunjuk Pembuktian:
- Harus dibuktikan operasi
 merupakan operasi biner (tertutup dan well-defined). Untuk membuktikan sifat tertutup, harus ditunjukkan bahwa
merupakan operasi biner (tertutup dan well-defined). Untuk membuktikan sifat tertutup, harus ditunjukkan bahwa  dan
dan  . Untuk membuktikan sifat well-defined, , diambil sebarang
. Untuk membuktikan sifat well-defined, , diambil sebarang 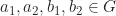 dengan
dengan  dan
dan  , harus ditunjukkan
, harus ditunjukkan  .
. - Ditunjukkan operasi * bersifat asosiatif.
- Dicari elemen netralnya, yakni dengan langkah pertama memisalkan
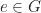 adalah elemen yang bersifat
adalah elemen yang bersifat 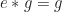 , dan selanjutnya diuraikan sehingga akan diperoleh bentuk dari elemen
, dan selanjutnya diuraikan sehingga akan diperoleh bentuk dari elemen  tersebut. Perlu dicek juga apakah
tersebut. Perlu dicek juga apakah  yang diperoleh tersebut memenuhi sifat
yang diperoleh tersebut memenuhi sifat 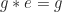 .
. - Diambil sebarang elemen
 . Dicari invers dari elemen
. Dicari invers dari elemen 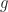 , yakni dengan langkah pertama memisalkan
, yakni dengan langkah pertama memisalkan 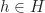 adalah elemen yang bersifat
adalah elemen yang bersifat 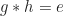 , dan selanjutnya diuraikan sehingga diperoleh bentuk dari elemen
, dan selanjutnya diuraikan sehingga diperoleh bentuk dari elemen 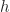 tersebut. Perlu dicek juga apakah
tersebut. Perlu dicek juga apakah 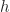 yang diperoleh tersebut memenuhi sifat
yang diperoleh tersebut memenuhi sifat 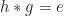 .
.
- Harus dibuktikan operasi
- Himpunan semua matriks berukuran
 atas
atas 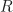 , dinotasikan
, dinotasikan 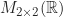 , merupakan grup (komutatif) terhadap operasi penjumlahan matriks
, merupakan grup (komutatif) terhadap operasi penjumlahan matriks  . Secara umum,
. Secara umum,  merupakan grup (komutatif).
merupakan grup (komutatif). - Himpunan
 merupakan grup (tidak komutatif) terhadap operasi perkalian matriks
merupakan grup (tidak komutatif) terhadap operasi perkalian matriks  . Secara umum,
. Secara umum,
![Rendered by QuickLaTeX.com \[G'=\{A\in M_{n\times n}(R)\mid \det(A)=1\}\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-fd3469241e167eeaac05f95a8d5bf590_l3.png)
merupakan grup (tidak komutatif) terhadap operasi perkalian matriks.
- Himpunan
 merupakan grup (tidak komutatif) terhadap operasi perkalian matriks
merupakan grup (tidak komutatif) terhadap operasi perkalian matriks  .
. - Himpunan
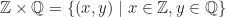 merupakan grup (komutatif) terhadap operasi
merupakan grup (komutatif) terhadap operasi  dengan definisi
dengan definisi
![Rendered by QuickLaTeX.com \[(a,b)*(x,y)=(a+x,b+y)\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-355d98f68173d1725d4d48ecd884c0d2_l3.png)
untuk setiap
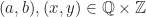 .
. - Misalkan
 dan
dan  keduanya adalah grup. Himpunan
keduanya adalah grup. Himpunan
![Rendered by QuickLaTeX.com \[G\times H=\{(x,y)\mid x\in G,y\in H\}\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-908b3e3f9053d69aa3ffe87b89d0babd_l3.png)
merupakan grup terhadap operasi
 dengan definisi
dengan definisi ![Rendered by QuickLaTeX.com \[(a,b)*(x,y)=(a*_{G}x,b*_{H}y)\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d3519212e91be14b62b688ada6a0dd08_l3.png)
untuk setiap
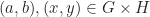 .
. - Misalkan
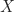 adalah sebarang himpunan tak kosong, dan
adalah sebarang himpunan tak kosong, dan 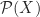 adalah koleksi semua himpunan bagian dari
adalah koleksi semua himpunan bagian dari 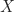 . Didefinisikan operasi biner
. Didefinisikan operasi biner  pada
pada 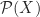 , yaitu
, yaitu 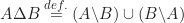 untuk setiap
untuk setiap  . Dapat dibuktikan bahwa
. Dapat dibuktikan bahwa 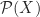 terhadap operasi
terhadap operasi  merupakan grup komutatif.
merupakan grup komutatif. - Himpunan
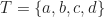 merupakan grup terhadap operasi biner yang didefinisikan pada Tabel Cayley berikut:
merupakan grup terhadap operasi biner yang didefinisikan pada Tabel Cayley berikut:
1Pada beberapa referensi/buku, ketika operasi * sudah jelas dikatakan merupakan operasi biner, aksioma ketertutupan ini kadang tidak dituliskan.
