Misalkan ![]() dan
dan ![]() adalah dua himpunan tak kosong. Suatu relasi
adalah dua himpunan tak kosong. Suatu relasi ![]() dari
dari ![]() ke
ke ![]() merupakan suatu himpunan bagian dari
merupakan suatu himpunan bagian dari ![]() . Selanjutnya jika
. Selanjutnya jika ![]() , kita katakan bahwa
, kita katakan bahwa ![]() berada dalam relasi
berada dalam relasi ![]() dengan
dengan ![]() , dan cukup dituliskan dengan
, dan cukup dituliskan dengan ![]() .
.
Sebagai contoh, jika ![]() merupakan himpunan semua bilangan asli dan
merupakan himpunan semua bilangan asli dan ![]() adalah himpunan semua bilangan bulat. Sudah kita ketahui bahwa untuk setiap bilangan asli
adalah himpunan semua bilangan bulat. Sudah kita ketahui bahwa untuk setiap bilangan asli ![]() pasti mempunyai kelipatan. Dari sini, jika untuk setiap
pasti mempunyai kelipatan. Dari sini, jika untuk setiap ![]() dan
dan ![]() didefinisikan
didefinisikan ![]() jika
jika ![]() untuk suatu bilangan bulat
untuk suatu bilangan bulat ![]() maka diperoleh
maka diperoleh
![]()
Dalam relasi ini, ![]() dan
dan ![]() berada dalam
berada dalam ![]() tetapi
tetapi ![]() tidak berada dalam
tidak berada dalam ![]() .
.
Sebagai contoh selanjutnya, diperhatikan himpunan semua garis lurus pada bidang datar, yakni ![]() . Pada
. Pada ![]() dapat didefinisikan relasi sejajar
dapat didefinisikan relasi sejajar ![]() dan tegak lurus
dan tegak lurus ![]() . Sebut relasi
. Sebut relasi ![]() dan
dan ![]() pada
pada ![]() didefinisikan sebagai berikut untuk sebarang garis lurus
didefinisikan sebagai berikut untuk sebarang garis lurus ![]() dan
dan ![]() di
di ![]() ,
, ![]() jika dan hanya jika
jika dan hanya jika ![]() dan
dan ![]() jika dan hanya jika
jika dan hanya jika ![]() . Jika diambil
. Jika diambil ![]() ,
, ![]() dan
dan ![]() , maka diperoleh
, maka diperoleh ![]() yang artinya
yang artinya ![]() dan
dan ![]() yang artinya
yang artinya ![]() .
.
Dari relasi ![]() dan
dan ![]() di atas, dapat diperoleh beberapa perbedaan, yakni:
di atas, dapat diperoleh beberapa perbedaan, yakni:
- Untuk setiap
 berlaku
berlaku  , tetapi tidak berlaku
, tetapi tidak berlaku  .
. - Untuk setiap
 , jika
, jika  maka berlaku
maka berlaku  . Sifat ini juga berlaku pada relasi
. Sifat ini juga berlaku pada relasi  , yakni untuk setiap
, yakni untuk setiap  , jika
, jika  maka berlaku
maka berlaku  .
. - Untuk setiap
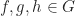 , jika
, jika  dan
dan  maka berlaku
maka berlaku  . Sifat ini tidak berlaku pada relasi
. Sifat ini tidak berlaku pada relasi  , yakni jika
, yakni jika  dan
dan  , maka
, maka 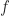 tidak akan tegak lurus dengan
tidak akan tegak lurus dengan 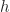 .
.
Dari tiga fenomena di atas, berikut didefinisikan relasi refleksif, simetris, dan transitif, serta relasi yang memenuhi ketiga jenis relasi tersebut.
Definisi 1. Diberikan relasi
|
Dari urian di atas, dapat diperoleh bahwa relasi ![]() merupakan relasi ekuivalensi pada
merupakan relasi ekuivalensi pada ![]() tetapi relasi
tetapi relasi ![]() bukan merupakan relasi ekuivalensi pada
bukan merupakan relasi ekuivalensi pada ![]() .
.
Supaya lebih memahami mengenai relasi ekuivalensi, diperhatikan contoh berikut ini.
Contoh 2. Diberikan relasi ![]() pada himpunan semua bilangan bulat
pada himpunan semua bilangan bulat ![]() yang didefinisikan sebagai berikut :
yang didefinisikan sebagai berikut :
![]()
untuk setiap ![]() .
.
Bukti.
- Dibuktikan
 relasi refleksif. Untuk sebarang
relasi refleksif. Untuk sebarang 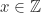 berlaku
berlaku  sebab
sebab  . Jadi
. Jadi  merupakan relasi refleksif.
merupakan relasi refleksif. - Dibuktikan
 relasi simetris. Diambil sebarang
relasi simetris. Diambil sebarang  dengan
dengan 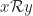 , artinya
, artinya  . Diperhatikan bahwa
. Diperhatikan bahwa  , sehingga
, sehingga 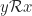 . Jadi
. Jadi  merupakan relasi simetris.
merupakan relasi simetris. - Dibuktikan
 relasi transitif. Diambil sebrang
relasi transitif. Diambil sebrang 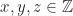 dengan
dengan 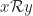 dan
dan  . Dari
. Dari 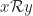 diperoleh
diperoleh  . Di lain pihak, dari
. Di lain pihak, dari  diperoleh
diperoleh  . Dengan demikian diperoleh
. Dengan demikian diperoleh  , dengan kata lain
, dengan kata lain  . Diperoleh
. Diperoleh 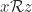 , jadi terbukti
, jadi terbukti  relasi transitif.
relasi transitif.
Dari (1), (2), dan (3), diperoleh bahwa ![]() merupakan relasi ekuivalensi.
merupakan relasi ekuivalensi.
![]()
