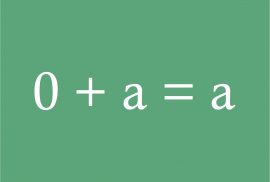Kita perhatikan kembali bahwa pada artikel sebelumnya telah dibahas definisi grup yang merupakan abstraksi dari fenomena-fenomena yang kita temui dalam bermatematika di kehidupan sehari-hari, salah satunya adalah fenomena dalam himpunan $\Z=\{\cdots, -3,-2.-1,0,1,2,3\cdots \}$ yang dilengkapi (more…)
Kita perhatikan kembali bahwa pada artikel sebelumnya telah dibahas definisi grup yang merupakan abstraksi dari fenomena-fenomena yang kita temui dalam bermatematika di kehidupan sehari-hari, salah satunya adalah fenomena dalam himpunan $\Z=\{\cdots, -3,-2.-1,0,1,2,3\cdots \}$ yang dilengkapi (more…)
Pada artikel sebelumnya (link Definisi Grup), “grup” merupakan merupakan suatu struktur yang merupakan suatu bentuk abstraksi dari kejadian yang kita temui pada himpunan bilangan bulat $\Z$ terhadap operasi penjumlahan $+$. Secara ringkas, grup merupakan suatu himpunan tak kosong yang dilengkapi suatu operasi biner dan memenuhi beberapa aksioma tertentu. Ada banyak contoh grup yang dapat kita temukan dalam kehidupan sehari-hari, misal: grup $(\mathbb{Z},+)$, $(\mathbb{Q},+)$, $(\mathbb{R},+)$, $(M_{2\times 2}(\mathbb{R}),+)$, dan lain sebagainya. Namun kenyataannya ada banyak himpunan yang dilengkapi dengan dua operasi biner dan memenuhi beberapa aksioma tertentu. Sebagai contoh, kita perhatikan himpunan $\Z$ dilengkapi operasi penjumlahan $+$ dan operasi perkalian $\cdot$.
 Dalam artikel ini kita akan membahas tentang definisi dari salah satu jenis struktur aljabar, yakni grup. Dalam konteks ini, “grup” hanyalah suatu nama dari sistem yang akan kita pelajari. Seperti yang telah (more…)
Dalam artikel ini kita akan membahas tentang definisi dari salah satu jenis struktur aljabar, yakni grup. Dalam konteks ini, “grup” hanyalah suatu nama dari sistem yang akan kita pelajari. Seperti yang telah (more…)
Misalkan $A$ dan $B$ adalah dua himpunan tak kosong. Suatu relasi $\mathcal{R}$ dari $A$ ke $B$ merupakan suatu himpunan bagian dari $A\times B$. Selanjutnya jika $(a,b)\in \mathcal{R}$, kita katakan bahwa $a$ berada dalam relasi $\mathcal{R}$ dengan $b$, dan cukup dituliskan dengan $a\mathcal{R}b$.
 Dalam kehidupan sehari-hari, kita telah mengenal dan menggunakan berbagai operasi bilangan. Untuk lebih mudahnya, kita dapat mengambil satu contoh, yaitu operasi penjumlahan bilangan bulat, yang sering kita gunakan dalam menghitung banyaknya uang (rupiah) yang kita punyai. Apabila kita mempunyai satu lembar (more…)
Dalam kehidupan sehari-hari, kita telah mengenal dan menggunakan berbagai operasi bilangan. Untuk lebih mudahnya, kita dapat mengambil satu contoh, yaitu operasi penjumlahan bilangan bulat, yang sering kita gunakan dalam menghitung banyaknya uang (rupiah) yang kita punyai. Apabila kita mempunyai satu lembar (more…)