Misalkan diberikan grup ![]() dan subgrup
dan subgrup ![]() di
di ![]() . Untuk setiap
. Untuk setiap ![]() , dapat dibentuk himpunan
, dapat dibentuk himpunan ![]() dan
dan ![]() dengan
dengan
![]()
Selanjutnya dibentuk himpunan-himpunan berikut:
![]()
Lebih lanjut, elemen-elemen di ![]() dan
dan ![]() berturut-turut disebut koset kanan dan koset kiri.
berturut-turut disebut koset kanan dan koset kiri.
Pertanyaan: Apakah pada himpunan ![]() [himpunan
[himpunan ![]() ] tersebut dapat didefinisikan operasi biner
] tersebut dapat didefinisikan operasi biner ![]() [operasi biner
[operasi biner ![]() ] sedemikian sehingga
] sedemikian sehingga ![]() merupakan grup [
merupakan grup [![]() merupakan grup)]?
merupakan grup)]?
Misal diambil sebarang dua koset kanan ![]() dan
dan ![]() di
di ![]() . Untuk mengoperasikan kedua koset tersebut, cara yang paling mudah adalah dengan mendefinisikan
. Untuk mengoperasikan kedua koset tersebut, cara yang paling mudah adalah dengan mendefinisikan
![]()
Pertanyaan: Apakah operasi ![]() merupakan operasi biner pada himpunan
merupakan operasi biner pada himpunan ![]() ?
?
Mudah dipahami bahwa operasi ![]() tertutup pada himpunan
tertutup pada himpunan ![]() .
.
Misal diambil sebarang ![]() dengan
dengan ![]() dan
dan ![]() , yang berarti
, yang berarti ![]() dan
dan ![]() . Karena
. Karena ![]() dan
dan ![]() , diperoleh
, diperoleh ![]() dan
dan ![]() , untuk suatu
, untuk suatu ![]() .
.
Operasi ![]() well-defined jika
well-defined jika
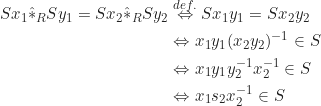
Jadi, operasi ![]() well-defined jika
well-defined jika ![]() .
.
Perhatikan: ![]() dan
dan ![]() , sehingga
, sehingga ![]() belum tentu merupakan anggota dari
belum tentu merupakan anggota dari ![]() . Lebih lanjut,
. Lebih lanjut, ![]() belum tentu merupakan anggota dari
belum tentu merupakan anggota dari ![]() .
.
Kesimpulan: Operasi ![]() belum tentu well-defined.
belum tentu well-defined.
Jika ![]() adalah grup komutatif, maka jelas berlaku
adalah grup komutatif, maka jelas berlaku ![]() sebab
sebab ![]() dan
dan ![]() . Akibatnya, jika
. Akibatnya, jika ![]() adalah grup komutatif, maka operasi
adalah grup komutatif, maka operasi ![]() well-defined. Akan tetapi syarat bahwa
well-defined. Akan tetapi syarat bahwa ![]() harus grup komutatif dinilai sebagai syarat yang terlalu kuat. Berdasarkan fenomena di atas, memotifasi untuk mendefinisikan subgrup baru yang memenuhi kondisi supaya operasi
harus grup komutatif dinilai sebagai syarat yang terlalu kuat. Berdasarkan fenomena di atas, memotifasi untuk mendefinisikan subgrup baru yang memenuhi kondisi supaya operasi ![]() well-defined.
well-defined.
| Definisi 1. Misal |
Syarat Perlu Dan Cukup Dari Subgrup Normal:
| Teorema 2. Misalkan |
Contoh 3.
- Setiap subgrup dari grup komutatif merupakan subgrup normal.
- Mudah dipahami bahwa
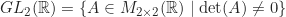 merupakan grup terhadap operasi perkalian matriks, dan
merupakan grup terhadap operasi perkalian matriks, dan 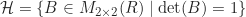 merupakan subgrup dari
merupakan subgrup dari 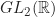 . Dapat dibuktikan
. Dapat dibuktikan 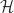 merupakan subgrup normal.
merupakan subgrup normal.
Bukti. Diambil sebarang . Akan dibuktikan
. Akan dibuktikan  . Diambil sebarang
. Diambil sebarang 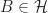 , berarti
, berarti 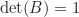 . Akan ditunjukkan
. Akan ditunjukkan  . Mudah dipahami
. Mudah dipahami

Jadi,
 . Berdasarkan SPC subgrup normal, berakibat
. Berdasarkan SPC subgrup normal, berakibat 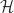 merupakan subgrup normal.
merupakan subgrup normal. 
Grup Faktor
Kita kembali ke pembahasan sebelumnya tentang pembentukan grup menggunakan himpunan ![]() dan operasi
dan operasi ![]() . Misalkan dalam pembentukan grup tersebut diberi tambahan syarat pada subgrup
. Misalkan dalam pembentukan grup tersebut diberi tambahan syarat pada subgrup ![]() , yakni dimisalkan
, yakni dimisalkan ![]() adalah subgrup normal.
adalah subgrup normal.
Perhatikan: Jika ![]() adalah subgrup normal,
adalah subgrup normal, ![]() , dan
, dan ![]() , maka berlaku
, maka berlaku ![]() , sehingga berakibat
, sehingga berakibat ![]() untuk suatu
untuk suatu ![]() . Dengan demikian,
. Dengan demikian, ![]() .
.
Kesimpulan: Jika ![]() adalah subgrup normal, maka dapat dijamin bahwa
adalah subgrup normal, maka dapat dijamin bahwa ![]() , yang ekuivalen mengatakan bahwa operasi
, yang ekuivalen mengatakan bahwa operasi ![]() well-defined.
well-defined.
Sebagai catatan, jika ![]() adalah subgrup normal di
adalah subgrup normal di ![]() , maka jelas berlaku
, maka jelas berlaku ![]() untuk setiap
untuk setiap ![]() . Hal ini berakibat himpunan-himpunan
. Hal ini berakibat himpunan-himpunan ![]() sama dengan
sama dengan ![]() yang selanjutnya dinotasikan
yang selanjutnya dinotasikan ![]() , dan operasi
, dan operasi ![]() sama dengan operasi
sama dengan operasi ![]() dapat ditulis dengan notasi yang sama, yaitu
dapat ditulis dengan notasi yang sama, yaitu ![]() .
.
Pertanyaan: Apakah himpunan ![]() terhadap operasi biner
terhadap operasi biner ![]() merupakan grup?
merupakan grup?
Dibuktikan bahwa:
- operasi
 bersifat asosiatif;
bersifat asosiatif;
untuk sebarang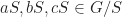 berlaku
berlaku
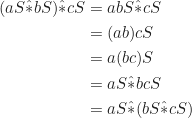
- adanya suatu elemen netral di
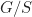 terhadap operasi
terhadap operasi  ;
;
terdapat sehingga untuk setiap
sehingga untuk setiap  berlaku
berlaku
![Rendered by QuickLaTeX.com \[e_{G}\hat{*}aS=e_{G}aS=aS=ae_{G}S=aS\hat{*}e_{G}S\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-aa4cb40b22441b2331754a7d8bf1b040_l3.png)
- ntuk setiap elemen di
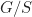 punya invers terhadap operasi
punya invers terhadap operasi  ;
;
untuk sebarang terdapat
terdapat 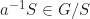 sedemikian sehingga
sedemikian sehingga
![Rendered by QuickLaTeX.com \[aS\hat{*}a^{-1}S=aa^{-1}S=e_{G}S~\text{dan}~a^{-1}S\hat{*}aS=a^{-1}aS=e_{G}S\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-73fefbea908bc33acac6cd45f7f346e7_l3.png)
Jadi, ![]() terhadap operasi biner
terhadap operasi biner ![]() merupakan grup, yang selanjutnya dinotasikan
merupakan grup, yang selanjutnya dinotasikan
![]()
dan disebut Grup Faktor dari ![]() yang terbentuk oleh subgrup
yang terbentuk oleh subgrup ![]() .
.
Contoh 4. Misal diambil subgrup ![]() di dalam grup
di dalam grup ![]() . Jelas
. Jelas ![]() adalah subgrup normal, sebab
adalah subgrup normal, sebab ![]() adalah grup komutatif. Grup faktor yang terbentuk adalah
adalah grup komutatif. Grup faktor yang terbentuk adalah
![]()
Secara umum, jika diambil subgrup ![]() di dalam grup
di dalam grup ![]() , maka grup faktor yang terbentuk adalah
, maka grup faktor yang terbentuk adalah
![]()
