Misal diberikan grup ![]() dan himpunan bagian tak kosong
dan himpunan bagian tak kosong ![]() . Ada dua kemungkinan yang terjadi pada
. Ada dua kemungkinan yang terjadi pada ![]() , yaitu
, yaitu ![]() merupakan subgrup atau
merupakan subgrup atau ![]() bukan subgrup.
bukan subgrup.
Pertanyaan: Apakah selalu bisa ditemukan subgrup yang memuat ![]() ?
?
Jawaban dari pertanyaan tersebut adalah “Ya, selalu bisa. Subgrup yang memuat ![]() adalah
adalah ![]() .”
.”
Pertanyaan di atas tentu saja kurang menarik sebab jawabannya sangat trivial. Bagaimanakan jika pertanyaannya diganti menjadi seperti ini?
Pertanyaan: Apakah selalu bisa ditemukan subgrup \underline{terkecil} yang memuat ![]() ?
?
Maksud dari kata “terkecil” dalam pertanyaan tersebut adalah himpunan (subgrup) yang paling kecil relatif terhadap relasi urutan ![]() . Untuk menjawab pertanyaan itu, perhatikan penjelasan berikut.
. Untuk menjawab pertanyaan itu, perhatikan penjelasan berikut.
- Jika
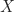 adalah subgrup, maka subgrup terkecil di
adalah subgrup, maka subgrup terkecil di  yang memuat
yang memuat 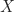 adalah subgrup
adalah subgrup 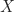 itu sendiri.
itu sendiri. - Jika
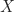 bukan subgrup, maka kita selalu dapat menentukan subgrup terkecil di
bukan subgrup, maka kita selalu dapat menentukan subgrup terkecil di  yang memuat
yang memuat 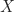 , yaitu dengan cara mengumpulkan semua subgrup di
, yaitu dengan cara mengumpulkan semua subgrup di  yang memuat
yang memuat 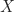 dan selanjutnya memilih subgrup yang paling kecil di antara subgrup-subgrup tersebut. Cara memilih subgrup yang paling kecil tersebut dapat dilakukan dengan cara mengambil subgrup yang terbentuk dari irisan semua subgrup yang kita kumpulkan tadi. (Ingat: irisan dari subgrup-subgrup merupakan subgrup.)
dan selanjutnya memilih subgrup yang paling kecil di antara subgrup-subgrup tersebut. Cara memilih subgrup yang paling kecil tersebut dapat dilakukan dengan cara mengambil subgrup yang terbentuk dari irisan semua subgrup yang kita kumpulkan tadi. (Ingat: irisan dari subgrup-subgrup merupakan subgrup.)
Konstruksi Subgrup Terkecil di ![]() Yang Memuat
Yang Memuat ![]()
- Dihimpun semua subgrup di
 yang memuat
yang memuat 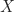 , yaitu dibentuk himpunan
, yaitu dibentuk himpunan
![Rendered by QuickLaTeX.com \[\mathcal{K}=\{H\subseteq G\mid H\text{ subgrup }, X\subseteq H\}.\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-7abda4a7a6b6640d07888969b862334a_l3.png)
- Iriskan semua subgrup di
 , yaitu
, yaitu 
Himpunan merupakan subgrup terkecil di
merupakan subgrup terkecil di  yang memuat
yang memuat 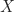 .
.
Pertanyaan Selanjutnya: Bagaimanakah bentuk anggota-anggota di dalam ![]() ?
?
 untuk setiap
untuk setiap 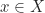 , sebab
, sebab  .
.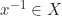 untuk setiap
untuk setiap 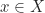 , sebab
, sebab  adalah subgrup.
adalah subgrup.
Dengan demikian, dan
dan  termuat di
termuat di  untuk setiap
untuk setiap 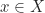 .
.- Karena
 adalah subgrup, diperoleh
adalah subgrup, diperoleh
![Rendered by QuickLaTeX.com \[x_{1}^{t_{1}}x_{2}^{t_{2}}\cdots x_{n}^{t_{n}}\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-a9136e73411b49510e4d5dbe493ee213_l3.png)
termuat di
 , untuk setiap
, untuk setiap 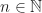 ,
,  .
.
Dibentuk himpunan
![]()
Dapat ditunjukkan bahwa ![]() , yaitu dengan menunjukkan:
, yaitu dengan menunjukkan:
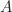 merupakan subgrup dari
merupakan subgrup dari 

- Subgrup
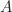 merupakan yang terkecil di antara subgrup-subgrup dari
merupakan yang terkecil di antara subgrup-subgrup dari  yang memuat
yang memuat 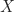 , yaitu ditunjukkan untuk sebarang subgrup
, yaitu ditunjukkan untuk sebarang subgrup 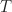 di
di  ,
,
jika  maka
maka  .
.
| Definisi 1. Misalkan Subgrup terkecil di |
Jadi, untuk ![]() diperoleh kesimpulan
diperoleh kesimpulan
![]()
Ada dua kemungkinan yang terjadi dengan ![]() jika dibandingkan dengan himpunan
jika dibandingkan dengan himpunan ![]() , yaitu
, yaitu ![]() atau
atau ![]() . Apabila yang terjadi
. Apabila yang terjadi ![]() , maka
, maka ![]() disebut himpunan pembangun (generator) dari grup
disebut himpunan pembangun (generator) dari grup ![]() .
.
Contoh 2.
- Grup
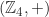 merupakan grup yang dibangun oleh
merupakan grup yang dibangun oleh 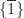 , sebab
, sebab
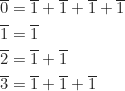
Jadi,
 .
. - Grup
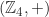 juga merupakan grup yang dibangun oleh
juga merupakan grup yang dibangun oleh  , sebab
, sebab
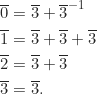
Jadi,
 .
. - Diberikan grup
![Rendered by QuickLaTeX.com \[V=\left\{A_1=\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}, A_2=\begin{bmatrix}-1 & 0\\0 & 1\end{bmatrix}, A_3=\begin{bmatrix}1 & 0\\0 & -1\end{bmatrix}, A_4=\begin{bmatrix}-1 & 0\\0 & -1\end{bmatrix}\right\}\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-56648bfaf322e426daf829e847698a2e_l3.png)
terhadap operasi perkalian matriks.\\
 \\
\\
 \\
\\
 \\
\\
 \\
\\
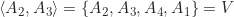
Sebagai latihan, tentukan subgrup dari ![]() :
:
- yang dibangun oleh
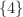
- yang dibangun oleh
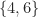 .
.
