Pada artikel sebelumnya (link Definisi Grup), “grup” merupakan merupakan suatu struktur yang merupakan suatu bentuk abstraksi dari kejadian yang kita temui pada himpunan bilangan bulat ![]() terhadap operasi penjumlahan
terhadap operasi penjumlahan ![]() . Secara ringkas, grup merupakan suatu himpunan tak kosong yang dilengkapi suatu operasi biner dan memenuhi beberapa aksioma tertentu. Ada banyak contoh grup yang dapat kita temukan dalam kehidupan sehari-hari, misal: grup
. Secara ringkas, grup merupakan suatu himpunan tak kosong yang dilengkapi suatu operasi biner dan memenuhi beberapa aksioma tertentu. Ada banyak contoh grup yang dapat kita temukan dalam kehidupan sehari-hari, misal: grup ![]() ,
, ![]() ,
, ![]() ,
, ![]() , dan lain sebagainya. Namun kenyataannya ada banyak himpunan yang dilengkapi dengan dua operasi biner dan memenuhi beberapa aksioma tertentu. Sebagai contoh, kita perhatikan himpunan
, dan lain sebagainya. Namun kenyataannya ada banyak himpunan yang dilengkapi dengan dua operasi biner dan memenuhi beberapa aksioma tertentu. Sebagai contoh, kita perhatikan himpunan ![]() dilengkapi operasi penjumlahan
dilengkapi operasi penjumlahan ![]() dan operasi perkalian
dan operasi perkalian ![]() .
.
Telah kita ketahui bahwa terhadap operasi penjumlahan ![]() dan perkalian
dan perkalian ![]() , himpunan bilangan bulat
, himpunan bilangan bulat ![]() bersifat:
bersifat:
- terhadap penjumlahan
 : (
: (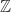 ,+) merupakan grup abelian
,+) merupakan grup abelian - terhadap perkalian
 }:
}: 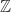 bersifat assosiatif
bersifat assosiatif
![Rendered by QuickLaTeX.com \[(\forall a,b,c \in \mathbb{Z})(a \cdot b)\cdot c=a \cdot(b\cdotc)\]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-2cdd6a6be6a9cf636d92b410f6eec9d5_l3.png)
- terhadap keduanya (penjumlahan dan perkalian):
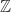 bersifat distributif kiri dan distributif kanan
bersifat distributif kiri dan distributif kanan

 .
.
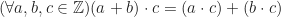
Dari fenomena sifat himpunan ![]() terhadap penjumlahan
terhadap penjumlahan ![]()
dan perkalian ![]() yang telah dijelaskan di atas, didefiniskan struktur abstrak yang disebut ring sebagai berikut.
yang telah dijelaskan di atas, didefiniskan struktur abstrak yang disebut ring sebagai berikut.
| Definisi 1. Misalkan operasi biner yang dinotasikan dengan disebut operasi penjumlahan dan perkalian. Himpunan jika:
|
Agar lebih efisien dalam penulisan, ring ![]() terhadap operasi penjumlahan
terhadap operasi penjumlahan ![]() dan perkalian
dan perkalian ![]() dinotasikan (
dinotasikan (![]() ). Nampak jelas bahwa definisi ring merupakan abstraksi dari suatu objek beserta sifat-sifatnya terhadap operasi penjumlahan dan perkalian, yakni himpunan bilangan bulat
). Nampak jelas bahwa definisi ring merupakan abstraksi dari suatu objek beserta sifat-sifatnya terhadap operasi penjumlahan dan perkalian, yakni himpunan bilangan bulat ![]() terhadap penjumlahan dan perkalian. Dengan demikian,
terhadap penjumlahan dan perkalian. Dengan demikian, ![]() merupakan contoh ring terhadap operasi penjumlahan dan
merupakan contoh ring terhadap operasi penjumlahan dan
perkalian, dan ditulis (![]() ).
).
Berikut contoh-contoh yang lain:
- Dengan mudah dapat ditunjukkan bahwa himpunan bilangan rasional
 , himpunan bilangan real
, himpunan bilangan real 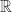 , dan himpunan bilangan kompleks
, dan himpunan bilangan kompleks  juga merupakan ring terhadap operasi
juga merupakan ring terhadap operasi
penjumlahan dan perkalian bilangan-bilangan yang sudah kita kenal sehari-hari. Oleh karena itu, dapat dituliskan dengan notasi
Ring (  ),
),
Ring (  ),
),
Ring (  ).
).Namun himpunan bilangan asli
 bukan merupakan ring sebab terhadap penjumlahan bukan merupakan grup.
bukan merupakan ring sebab terhadap penjumlahan bukan merupakan grup. - Pandang himpunan matriks bujursangkar berukuran
 dengan komponen-komponen bilangan real, yakni
dengan komponen-komponen bilangan real, yakni
![Rendered by QuickLaTeX.com \[ M_{2 \times 2}(\mathbb{R})=\left\{ \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} \mid a_{ij} \in \mathbb{R}, i,j=1,2 \right\}. \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-8972b2491d1b7015a5a9d578198b6166_l3.png)
Dari sifat-sifat penjumlahan dan perkalian matriks, dapat ditunjukkan bahwa
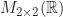 merupakan ring terhadap operasi penjumlahan dan perkalian matriks.Selanjutnya untuk setiap bilangan asli
merupakan ring terhadap operasi penjumlahan dan perkalian matriks.Selanjutnya untuk setiap bilangan asli 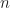 , dapat ditunjukkan bahwa
, dapat ditunjukkan bahwa![Rendered by QuickLaTeX.com \[ M_{n\times n}(\mathbb{R})=\left\{\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \cdots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}\mid a_{ij} \in \mathbb{R}\right\}. \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-27c5c42bf0c5ef7bf0847439a137c012_l3.png)
merupakan ring terhadap operasi terhadap operasi penjumlahan dan perkalian matriks.
Proses memperluas dari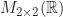 ke
ke  merupakan salah contoh proses generalisasi.
merupakan salah contoh proses generalisasi. - Pandang himpunan semua fungsi dari
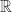 ke
ke 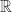 sebagai berikut
sebagai berikut
![Rendered by QuickLaTeX.com \[ F(\mathbb{R},\mathbb{R})=\{f: \mathbb{R} \rightarrow \mathbb{R}\mid f \; \text{fungsi}\}. \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-bab25c9973f403e0551bde3c5df58a35_l3.png)
Dari Kalkulus, kita dapat mendefinisikan operasi penjumlahan fungsi dan juga perkalian fungsi sebagai berikut. Untuk sebarang
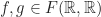 didefi\-nisikan
didefi\-nisikan  dan
dan 
sebagai berikut:![Rendered by QuickLaTeX.com \[ (f+g)(x)=f(x)+g(x) \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-08c59681198835e6f752672d40b2439d_l3.png)
dan
![Rendered by QuickLaTeX.com \[ (f\cdot g)(x)=f(x)\cdot g(x) \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-44f1dba34c0151ee0e74087b879f4274_l3.png)
untuk setiap
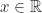 .
.
Dengan menggunakan sifat-sifat dalam kalkulus, dapat ditunjukkan bahwa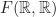 merupakan ring.
merupakan ring. - Diberikan himpunan kuasa dari
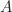 , yaitu himpunan semua himpunan bagian
, yaitu himpunan semua himpunan bagian 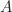 , yang dinotasikan
, yang dinotasikan
![Rendered by QuickLaTeX.com \[ 2^A=\{S \mid S \subseteq A\}. \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-0b2e115a083f08f76b3edab00c65ecf0_l3.png)
Dapat ditunjukkan bahwa
 merupakan ring, dengan operasi penjumlahan dan perkaliannya didefinisikan sebagai berikut:
merupakan ring, dengan operasi penjumlahan dan perkaliannya didefinisikan sebagai berikut:![Rendered by QuickLaTeX.com \[ (\forall S_1, S_2 \in 2^A) S_1+ S_2=(S_1-S_2)\cup (S_2-S_1) \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-cae6978d636cf47a0146cad039efa404_l3.png)
dan
![Rendered by QuickLaTeX.com \[ (\forall S_1, S_2 \in 2^A) S_1\cdot S_2=S_1\cap S_2 \]](https://strukturaljabar.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-71011c7965dc759613546f6a517e5187_l3.png)
